|
Author
|
Topic: Prob 8-6 answer
|
David Burch
|
 posted April 25, 2005 11:21 PM
posted April 25, 2005 11:21 PM


These details were not in the answers prior to April, 2005.
The first step of the problem asks us to identify the current stations shown in the chartlet using the list of stations. Refer to page 11 of chart problems book that lists the secondary stations.
Leg one is bounded by 3 stations, north of it is #1971, south of it is #1966, and the point nearly right on the leg that we can use for this prediction is #1941. So for leg one we use the values at #1941.
For leg 2, there is only one station near by, north of the leg, which is #1961 in our list. We will use that one for leg 2. Note that this station is about slack at the time the picture was made in the chart problems book.
Leg 3 has two stations, one northeast of it (#1956) and one about the same distance southwest of it (#1951) , so we will use the average of these two for the route.
These stations are all referenced to Rosario Strait data. The problem asks current values at mid point departing at 1000 PDT, August 8th 1999, and traveling at 3 kts.
Leg 1 is about 1.8 nmi (according to scale on the chartlet given, or if using electonic course just measure it precisely-- although precise results do not matter here.) At 3 kts we travel 20 min per mile, so 1.8/2 x 20 min = 18m so what is the current at #1941 at 1018?
At Rosario Strait on Aug 8 we get (adding one hour for PDT)
0634 2.9 kt Ebb
1042 Slack
1340 1.7 kt Flood
Our entire trip is leg 1 = 1.8nm, leg 2 = 2.3 nmi, and leg 3 = 2.0 nmi, for a total run of 6.1 nmi, and at 3 kts this is about 2 hours, so we do not care for now about predictions beyond 1340.... we should be there at roughly 1200, assuming no current, and we are now figuring roughly how long it will take in the anticipated current.
Now to apply the corrections to Rosario to get the values at #1941. From Table 2 we can make these corrections to get to the values at #1941: time of slack before the flood is the same and the ebb at #1941 is 0.5 times as strong and occurs 1h 23m earlier, so we have at station #1941:
0634 - 0123 = 0511 = 0.5 x 2.9 = 1.5 ebb @ 210 T
1042 + 0000 = 1042 = slack
1340 + 0114 = 1444 = 0.6 x 1.7 = 1.0 kt flood @ 035 T
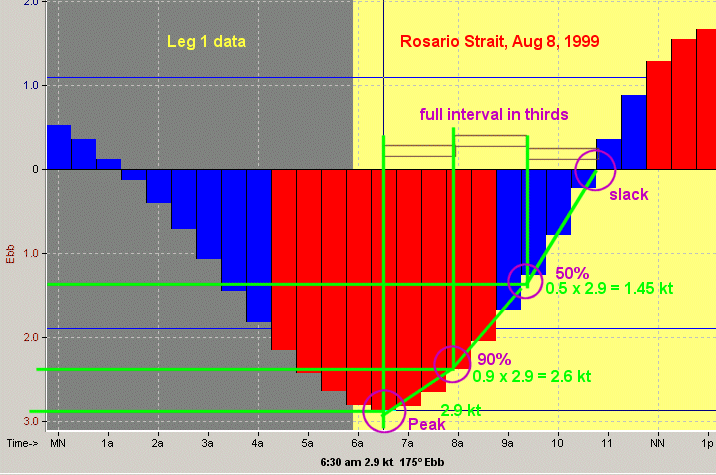
So the question now reads if the peak ebb is 1.5 kt at 0511 and the water is slack at 1042, what is the speed of the current at 1018. There are several ways to estimate this current -- the easiest is a software program that tells the current precisely where we want it when we want it, the next is an interpolator program like in our starpilot which will tells us the answer is 0.17 kt, but we want to do this by hand for now.
One method in the book is called the 50-90 rule--a rule which originated in the starpath classroom. We take 1042 - 0511 = 5h 31m and a third of that is about 110m = 1h 50m, so at 1042 - 0150 = 0852 the current is 0.75 kts, and we might guess a linear drop between 0.75 at 0852 and 0.0 at 1042, which is 0.75 kts in 110m, or = 0.007 kt per min, so 0852 to 1018 = 86 min and 86 x 0.007 = 0.60 kts, and 0.75 - 0.60 = 0.15 kts Ebb... not a very big current even at 3.0 kts... ie it is 0.15/3.0 = 5%.
From Table 2 we see that the direction of the max ebb at #1941 = 210 T, so the first answer is the current midway of the first leg is about 0.2 kts toward direction 210 T, and we can neglect this effect on our speed as we proceed to figure the next answer, midway on leg 2.
An illustration of the 50-90 rule and this problem is shown below.
Leg 1 is 1.8 mi at 20m/mile = 36m so we arrive at the start of leg 2 at 1036. For leg 2 we will use #1961, and at this station the ebb is 0.7 x the strength as Rosario and the time of ebb is 34m earlier and the slack before the flood is 01h 08m later, while the flood is 0.8 times larger and occurs 50 m later, so we have at station #1961:
0634 -0034 = 0600 = 0.7x2.9 = 2.0 kt ebb @ 190 T
1042 + 0108 = 1150 = slack
1340 + 0050 = 1430 = 0.8 1.7 = 1.4 kt flood @ 015 T
We are now in a region of strong current relative to our boat speed of 3 kts, but we are there at about the best time.
The leg is 2.3 miles long, so half way is about 1.2 mile which equals 1.2 x 20 m = 24m. With no current we would be there at about 1036 + 24 = 1059 which is about an hour before slack. In this case this will not be so bad, but in other cases this could be a concern for a vessel that is limited to 3.0 kts..
We can do the interpolation roughly, as 1150 is about 12, so the time interval slack to peak is 6 hr and a third of that is 2h, so at 10 the current is half of 2.0 kt = 1.0 kt. So we have 1.0 kt at 1000 and 0 at about 1200, so what is the current at 1059 which is about 11, and the the answer is about 0.5 kt at 190 T.
We see that the current is building. We now have 0.5 kt/3.0 kt = 17% , or a current of some 17% of our boat speed. We will come back to this, but we do know that we will need about a 6° correction for every 10% of current, so we are getting set now and our corrections will be slowing us down.
.
Leg 2 is 2.3 miles, or 46m with no current effect and we started it at 1036, so we will start Leg 3 at 1036 + 0046 = 1122. Leg 3 is 2 mi at 20m/mile = 40m so we arrive at the midpoint of Leg 3 at 1122 + 20 = 1144. For leg 3 we will use the average of #1951 and #1956. to do this, just average each of the sets of corrections. For exampe, one has an ebb that is 1.2 x Rosario and the other is 1.0, so we will use 1.1... one has an ebb direction of 215 T and the other 235 T, so we will use 325 T, and so on.
0634 +0003 = 0600 = 1.1 x 2.9 = 3.2 kt ebb @ 325 T
1042 + 0011 = 1053 = slack
1340 + 0022 = 1402 = 1.2 x 1.7 = 2.0 kt flood @ 055 T
We are now in a region of strong current relative to our boat speed of 3 kts, and our timing is begining to slip. Our estimates now are going to need some corrections when we are done. Using the same approach as before, we have about a 3 hour cycle (1053 to 1402) , so the current at an hour after slack (1153) is going to be about 1 kt at 055 T -- not taking into account the effect of the current getting there. So the first answer to the third leg would be about 1 kt at 055 T.
But this is sadly not a realistic answer as we are not going to ge there anywhere near 1144 as anticipated since we have to buck this current to get there as it builds.
For the chosen times, we will be at or near slack current for each leg, and with minimal correction for current is necessary for any of the three legs.We will arrive at Colville Island at about 1200 PDT, as we would have had there been no set and drift at all. However, had we departed only three hours later, at 3 kts we would not have been able to reach Colville Island at all. Here is an overview of the route. See chartlet and current plots.
Depart 1000 PDT on aug 8, 1999
wp 1 = 1000 PDT
leg 1 = 1.8 mi = 36m (course = 256 T)
wp 1.5 = 1018 current = 0.2 kt at 210T at station 1
leg 2 = 2.3 mi = 46m (course = 283 T)
wp 2.5 = 1059 current = 0.5 kt at 190T at station 2
leg 3 = 2.0 mi = 40m (course = 281 T)
wp 3.5 = 1142 current = 0.8 kt at 215T at station 3
wp 4 = 1202
The above values assume the current did not change your speed made good. At just 3 kts through the water, however, if we did choose to crab and go straight, we would be speeded up or slowed down a bit depending on whether the current is forward or aft of the beam. In all three legs it is near, but not exactly the beam in this example.
The computed or plotted SMG for each leg using the above currents including the correct course to steer to make good the desired course would be:
wp 1.5 smg = 3.14 CTS = 258.7 ie crab 3°
wp 2.5 smg = 2.93 CTS = 292.6 ie crab 10°
wp 3.5 smg = 3.24 CTS = 295.1 ie crab 14°
(If we used our shortcut trick of current/speed x 60 we would get 4, 10, and 16, which is fairly close to the above exact results.)
The neap-tide of Saturday the 21st of August gives us the least current of the two month period, and if we depart Deception Island at 0900 PDT we should experience slack water for our entire trip. Perhaps the greatest concern with this trip is collision avoidance, as we are crossing two major traffic lanes.
From: Starpath, Seattle, WA
|
|
|

 Topic Closed
Topic Closed


 Topic Closed
Topic Closed



 Topic Closed
Topic Closed


 Topic Closed
Topic Closed

