|
Author
|
Topic: Lunar distance using Stark's tables
|
navi
|
posted June 05, 2017 02:40 PM
Hello!
Thanks for your answers.
As you point out using UTC 2h0m0s for clearing means my Hc's are different from yours leading to another clearing result than you have leading to error.
Since the point of making a lunar is the find the time, does it make sense to do an iterative process?
Say as in my case I use the Hc's for UTC 2h0m0s and I get a time of UTC 2h36m47s, does it make sense to use that calculated time to find new Hc's and redo the clearing and get another time.
My reasoning is that if I only know a DR position and that the time is between UTC 2 and 3 I must start with some Hc's to get going. The first iteration giving me 2h36m47s is much closer to the true value (2h55m47s) than 2h0m0s so the Hc's will be closer the true time so the clearing will be better.
Then I get a new time and can redo this once again. Logically it should converge.
What do you think, does it make sense?
From: Chi
|
|
David Burch
|
posted June 05, 2017 03:21 PM
I think we should go back to the basics here and review what is going on.
in the lunar, we measure the distance between body and moon. then we clear the distance, which means account for all corrections to get the true observed distance, center to center of the two bodies. There are several factors that go into this, a large one being the limb used, i.e. in star to far edge of the moon, you have to take out the semi diameter to get to the center. on a close edge you have to add it. then there is refraction and a couple other small corrections, but you end up with cleared lunar distance. i think your result was 24 27.8’
This you found from a given DR and at a specific time. our job is to find either the correct time, i.e. error in what you used, or a corrected DR. These are equivalent.
once you know time used and cleared distance, then we simply compute what the cleared distance is over some time interval that spans what you used. Generally this is easiest using a whole hour of UTC, so you do the computation for whole hour before and whole hour after. this gives you two lunar distances.
You then just interpolate to find the right time. i.e. given T1 and LD1 and T2 and LD2, and your LDx, find the time TX that gives your Ldx. that is then the correct time, and the difference between that and the time you actually used is your error in time.
this last step of finding two LDs at two times does not require stark tables, you can just compute it as i did in a note above. Stark just gives you an easy way to do this without other tables of computation.
the time interval used for this last step interpolation does not matter. In the old days, the almanacs included precomputed distances for selected bodies every 3 hours.
From: Starpath, Seattle, WA
|
|
David Burch
|
posted June 05, 2017 03:25 PM
note we can think of this as finding Lon, as we can always know our true Lat without time. At sea any two stars will give your lat correct, or in a lunar if you measured Hs body and Hs moon, you could use those to find Lat. The Lon will be wrong by your time error, but the Lat will be right
From: Starpath, Seattle, WA
|
|
David Burch
|
posted June 05, 2017 03:54 PM
and to be a bit more specific about your comment: the Hc values do not enter in to the process at all. you do not need Hc to find the LDs being used for interpolation. it is just a great circle computation between the two GPs. In fact, as you have seen from the stark tables, you do not need the Hcs for finding the LD in the first place. These enter in arguments for the refraction and other moon corrections and do not have to be precise. If they did happen to be way off, then we could always iterate. ie, take known Lat (we can always assume we know that) then find watch error, then if large, we correct the watch time and do it again.
From: Starpath, Seattle, WA
|
|
navi
|
posted June 05, 2017 06:28 PM
Hi,
I recalculated with Hc's of 2h55m47s and got about 3 min error just like you.
In this case Hc moon is about 7 degree different between 2 and 2h55m47s that seems enough to throw of the clearing. Planet Hc is about 2 degrees different. Maybe in practice on either has a sea horizon or a watch with an error that is 5-10 min then the difference in Hc will be less dramatic.
In a few weeks I will be on the sea and will try out real Hc's. Lat 62 Lon 17E.
From: Chi
|
|
David Burch
|
posted June 05, 2017 06:36 PM
not exactly sure what you have done, but sounds like it is working for you.
Have a good voyage.
From: Starpath, Seattle, WA
|
|
navi
|
posted June 05, 2017 07:31 PM
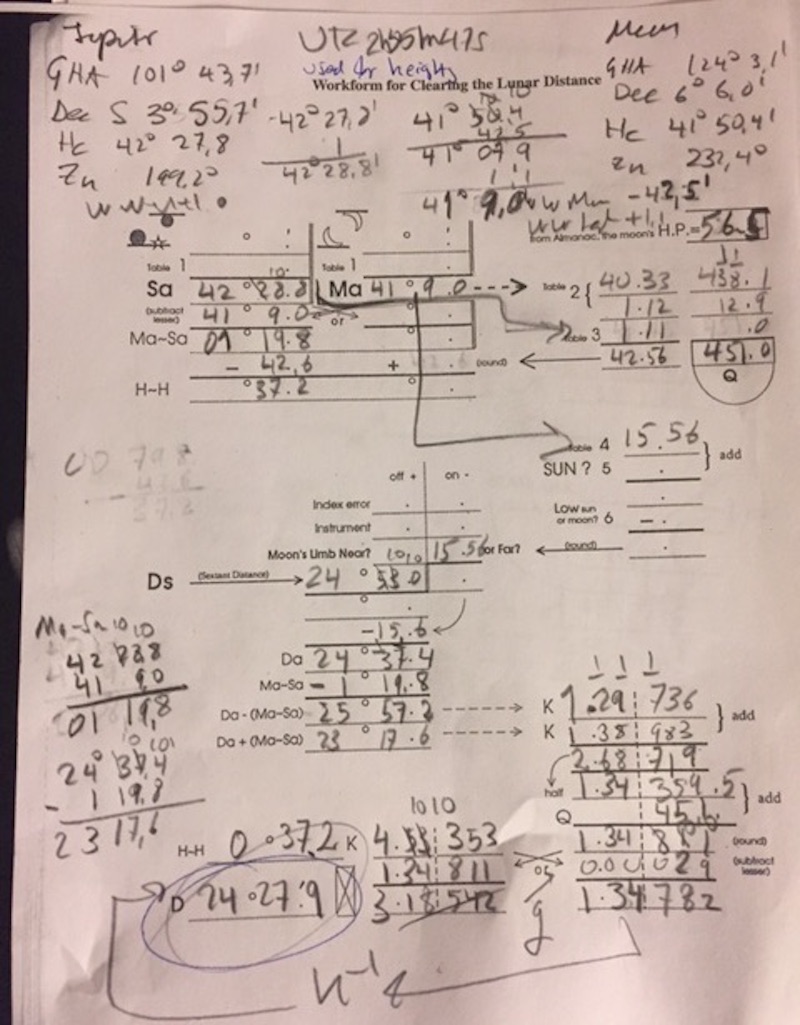
From: Chi
|
|
navi
|
posted June 05, 2017 07:39 PM
I did the same thing as you, that is using Hc's from UTC 2h55m47s. You got D= 24deg27.8' with your form I got 24deg27.9' as per the attached form.
From: Chi
|
|
David Burch
|
posted June 15, 2017 09:18 PM
Here is another solution using the Navigation Spreadsheets from Peter Hakel. A full tool kit of navigation computations. Note his lunar solution in this version requires either measured altitudes, or you have to back the Ha out of the Hc values. The Stark Tables does this with the "Wrong Way" table. See Steve Miller's article on the Stark Tables on how to use that and the other tables.
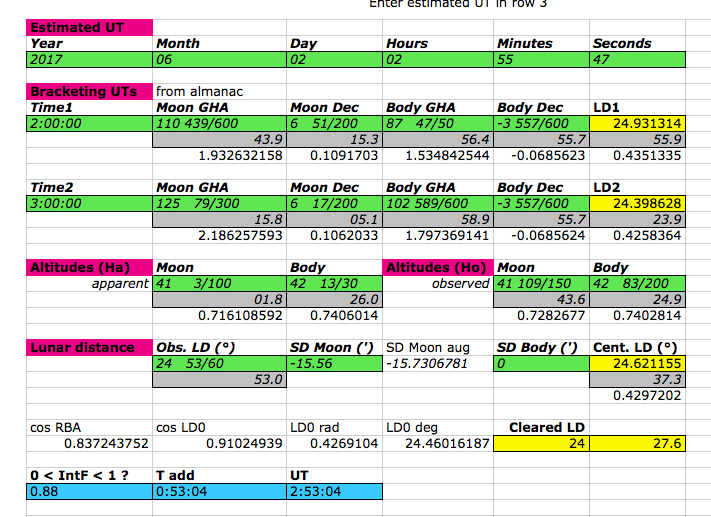
From: Starpath, Seattle, WA
|
|
|
