|
Author
|
Topic: Plane sailing in Bowditch, tricky interpolation
|
YMO 2013
|
 posted blank , 1920
posted blank , 1920


Was just going through para 2412 of Bowditch last edition,trying to solve example 2 through Traverse Tables (page 353). Did not really understand how it gets to D=244.3 mi by "interpolating for intermediate values": is it single linear or double or what?
Would really appreciate a detailed step by step solution
Many thanks in advance
From: Mediterranean
|
|
David Burch
|
 posted December 27, 2012 07:03 AM
posted December 27, 2012 07:03 AM


For some reason your questions are not posting properly, but our email copy works, so this is re-posted here for you. The other seems to be the same issue so we will look at this one and get back shortly.
From: Starpath, Seattle, WA
|
|
David Burch
|
 posted December 27, 2012 05:07 PM
posted December 27, 2012 05:07 PM


Thanks for the question and forcing us to look at these tables, which we rarely do anymore. First the right answer is easy to get, namely sqr root (136^2 + 203^2) = 244.346
Normally the Bowditch approach to a triple interpolation is to start with a base value and then make the two corrections to it. This is not exactly right, but all cel nav tests work doing this.
In this case, however, this does not work, so I must say i have no idea where they get the answer they do.
if you start with the base: d=244 dLat = 202.3 and dep = 136.4 and correct for dLat you get +.875, then correct for dep and you get - 0.80, so you are left with d=244.1.
It could be they knew the right answer, and just assumed it was right and wrote it down. Note that earlier they say the answer is 244.8 but that is definitely wrong.
There is really no need for Traverse Tables in modern times, as one can work these out to fractions of a mile with a cell phone, not to mention that we know now that these computations are not right in the first place because the earth is not round.
Essentially all GPS units will compute the proper ellipsoidal distances depending on the datum selected, normally WGS-84.
Sorry this is not much of an answer. I would hope that the various licensing agencies around the world would let this go. It even predates hand held calculators that do trig, ie early 70s.
From: Starpath, Seattle, WA
|
|
David Burch
|
 posted December 27, 2012 05:15 PM
posted December 27, 2012 05:15 PM


for the record here are the two interpolations using a smartphone app.
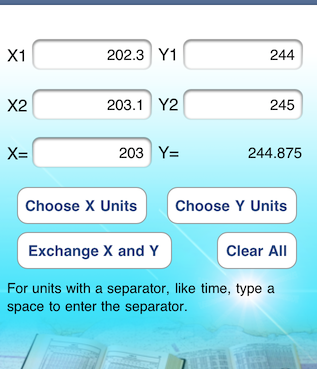
..
From: Starpath, Seattle, WA
|
|
David Burch
|
 posted December 27, 2012 05:17 PM
posted December 27, 2012 05:17 PM


the second one
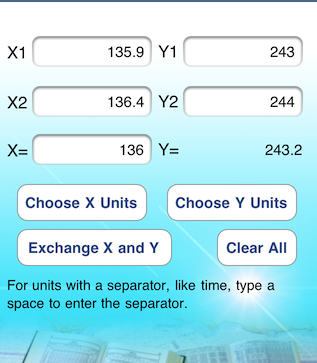
From: Starpath, Seattle, WA
|
|
David Burch
|
 posted December 28, 2012 01:06 PM
posted December 28, 2012 01:06 PM


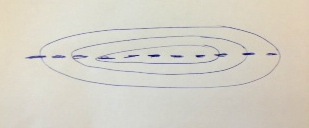
I see this dead horse is still moving, so here are some more notes, which i think show there is no logical way to interpolate these tables, but you could with a couple sketches (and no other computations) get a little bit better value.
This picture shows the two triangles from the double interpolation. we want distance A to B, which will see will be between 243.20 and 244.875.
One approximation would be swing the arc of the 243.20 and you see what we are missing is about the difference between the two departures, 1.34 nmi, thus an improved guess would be 243.2 + 1.3 = 244.5, compared to right answer of 244.35.
Message remains, better to solve this problem some other way and sell our traverse tables on ebay to historians.
From: Starpath, Seattle, WA
|
|
YMO 2013
|
 posted December 30, 2012 11:42 AM
posted December 30, 2012 11:42 AM


Thanks so much Instructor, your explanation was very clear and useful. You're right, in the GPS Era Traverse Tables are rather historians' stuff: my interest was actually more on a "paper-only-tech" side of sailing.
From: Mediterranean
|
|
David Burch
|
 posted December 30, 2012 12:07 PM
posted December 30, 2012 12:07 PM


That is a worthy goal, as all electronics are vulnerable. However, for paper-only these types of problems can be solved by plotting on universal plotting sheets or charts with results that are more than adequate. Thus in collecting the tables that would be needed to cover all non-electronic nav problems, we can still leave the traverse tables at home!
Something like Kolbe's Long Term Almanac is a tremendous tool for all-paper long term navigation. It is now available in hard back or paperback. There is a section in it that shows how to use the tables for great circle sailings.
Also keep in mind, that knowing the simple equations for mid-latitude sailing (Traverse Tables) one can solve these to high precision with an inexpensive slide rule, either the round kind or standard long one. These things are actually still for sale... and they do not take batteries! You can even do sight reduction with them, which means great circle sailing and so on.
Slide rules are a great tool for those who wish to be independent of electronics, yet still want to do navigation. The books can get very heavy and bulky.
From: Starpath, Seattle, WA
|
|
YMO 2013
|
 posted December 30, 2012 02:54 PM
posted December 30, 2012 02:54 PM


Thanks again, bright idea indeed. Will update my grab-bag and go through Kolbe's straight after I get my YMO ![[Smile]](smile.gif)
From: Mediterranean
|
|
|